In our previous newsletter, Henk Myburgh, CFA, explored different approaches to allocating capital across asset classes. Now, we turn our attention to a mathematical tool that can help guide allocations to individual investments: the Kelly Ratio.
Investment managers often dedicate substantial effort to identifying investments that satisfy their clients’ investment objectives. However, identifying these investments is only the first step in constructing a sensible investment portfolio.
Next, investment managers must decide how much of the limited investment capital at their disposal should be allocated to each investment identified.
- Should capital allocation be done in relation to the expected returns offered by each investment opportunity / option?
- This approach is flawed because predicting future relative returns accurately is nearly impossible.
- Should capital be allocated on an equal weight basis?
- This ignores the varying risks associated with each investment.
- Should capital simply be utilised to replicate an index?
- If so, why not just buy the index and avoid all the work done in the first step?
Clearly, a framework that is stable, sensible, and reliable to guide the capital allocation process is required.
The Kelly ratio is a method to decide how much available capital should be invested in an opportunity by maximising growth over time, without taking unnecessary risks.
The Origins of the Kelly Criterion
The Kelly Criterion was developed in 1956 by John L. Kelly Jr., a researcher at Bell Labs, as a method for optimising signal transmission over noisy communication channels. Mathematician and investor Edward Thorp later recognized its application in gambling and investing. Thorp applied the Kelly Criterion to blackjack, demonstrating its effectiveness in bet sizing, and later extended it to financial markets to enhance portfolio returns while controlling the risk of ruin.
The Kelly Formula in Investing
The Kelly formula is relatively simple:
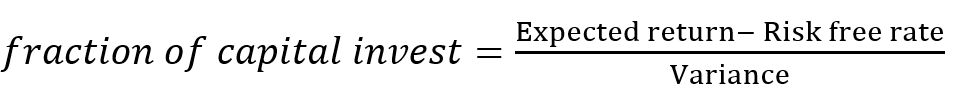
Notes: If the expected return is less than the risk-free rate, you should not invest as you can earn more without taking any risk. As the expected return increases, you should invest more, and as the variance (risk) increases you should invest less.
For example, if an asset has an expected annual return of 12%, a risk-free rate of 8%, and a variance of 0.09 (i.e., a volatility of 30%), the Kelly fraction would be:
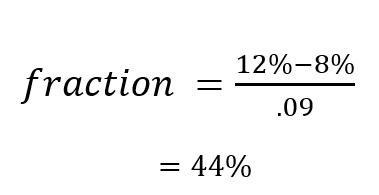
This suggests that an investor should invest 44% of capital. Outsized position sizes may not be practical due to risk constraints, so many investors use a fraction of the Kelly result to manage volatility.
The Risks of Over-Betting and the Half-Kelly Adjustment
One of the most important takeaways from the Kelly Criterion is that it provides an upper limit for allocation. Investing beyond this limit increases the probability of ruin – running out of capital due to compounding losses. Overexposure is a common pitfall in financial markets, as excessive position sizes can lead to catastrophic drawdowns.
While the full Kelly ratio theoretically maximises returns, it can also lead to high volatility and deep drawdowns.
A common practice is to use half-Kelly to balance returns with a smoother growth trajectory. Empirical studies suggest that half-Kelly allocations offer about three-quarters (75%) of the full-Kelly return with significantly lower risk. This adjustment helps mitigate the risk of ruin while still allowing for strong long-term capital growth.
Evaluating Opportunities
In practice, it is often difficult to estimate the expected return from an investment. If we decide on a fraction, for example 100%, we can express the half-Kelly ratio in terms of expected return. In this case, it becomes a required return to invest 100%.
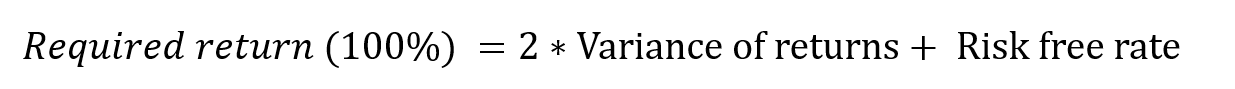
The graph below shows the minimum required return that would justify investing 100% of your capital for different levels of return volatility.
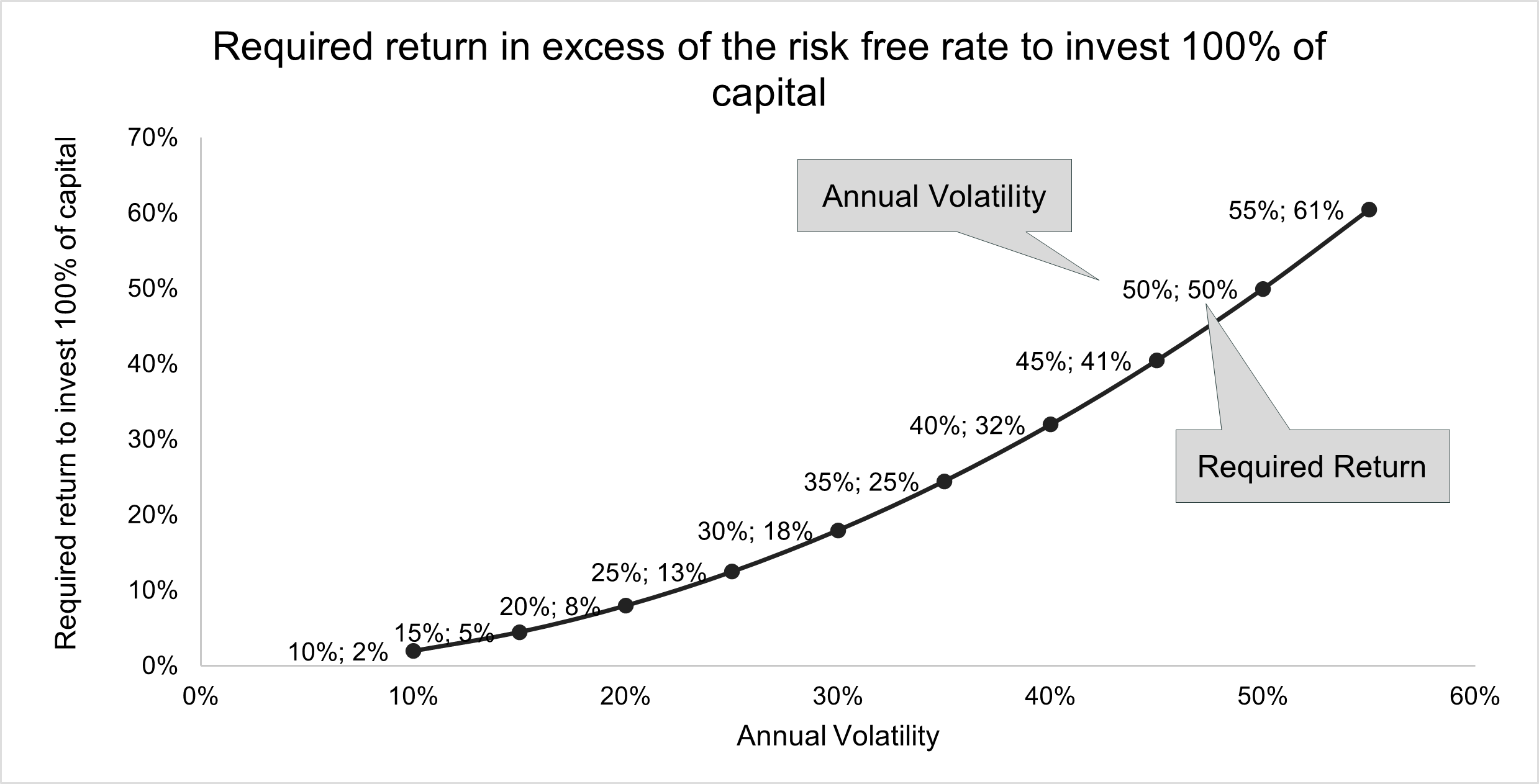
With the result from the calculation, you can evaluate whether the required return is reasonable or too high, based on your expectations.
Looking at the earlier example which has an annual volatility of 30%, the required return for a 100% investment is 18%, in excess of the risk free rate.
The required return including the risk free rate is: 18% + 8% = 26%
If the required return appears to be too high, it does not mean that you should abandon the investment, but rather that investing 100% of your capital is not sensible. On the other hand, if you believe that the required return is much less than your expectation, it indicates that it should be safe to invest 100% of capital.
This process can be replicated for any fraction of investment.
The Kelly ratio and Modern Portfolio Theory
The Kelly Criterion shares similarities with Harry Markowitz’s mean-variance optimisation, which forms the basis of Modern Portfolio Theory (MPT). Both approaches aim to maximise expected return, while controlling for risk. Notably, the MPT-optimal portfolio is the portfolio where the marginal Kelly ratio — the ratio of expected excess return to variance — is equal across all holdings. This means that an investor who optimises using MPT is, in effect, following a Kelly-optimal strategy in a well-diversified portfolio setting.
In the next and final instalment of this series, we will explore how the Kelly Criterion can be extended beyond single investments to optimise entire portfolios. By applying its principles across multiple assets, investors can strike a balance between maximising returns and managing risk in a diversified strategy.
